Dynamic games, large scale systems and optimization

( R. P. Hämäläinen, K. Berg, H. Ehtamo, J. Karelahti, M. Kitti, V. Mattila, J. Poropudas, T. Raivio, T. Tahvonen, K. Virtanen )

Dynamic game theory is related to the modelling of large scale systems which have independent decision makers or acting agents with individual payoff functions. In dynamic games, the decisions are made in multiple stages. In the games considered here the optimizations are done subject to a difference or differential equation describing the undelying dynamic system. Depending on the mode of interaction different solution concepts become applicable: noncooperative Nash equilibrium solution, of which special cases are maxmin and Stackelberg or leader-follower solutions, and cooperative and bargaining solutions. Our work dates back to the seventies and it stems from the tradition of differential games. Our emphasis is on theoretical research as well as on the interactive computer implementation of algorithms. Applications dealt with so far include, e.g., environmental and resource problems and energy management.

Dynamics and strategy of flight

( H. Ehtamo, R. P. Hämäläinen, J. Karelahti, V. Mattila, J. Poropudas, T. Raivio, T. Tahvonen, K. Virtanen )

In 1993, we initiated a project with the Finnish Air Force to study single aircraft performance optimization in conjunction with the modeling and simulation of antagonistic aerospace scenarios. In the project, optimal control theory and differential games as well as tools from decision theory are utilized in the modeling of aerospace problems.

Aircraft trajectory optimization

Numerical solution of optimal control problems has been based on the Pontryagin maximum principle, which leads to a highdimensional nonlinear multipoint boundary value problem. In P[EHT94] and R[EHT00a] we develop a continuation method for minimum time problems and apply it in calculating minimum-time-climb trajectories of a modern aircraft. Such a trajectory brings an aircraft from a given initial state to a specified altitude and velocity in the shortest possible time. In P[RAI96b], the approach is applied to the worst case analysis of aircraft trajectories in the horizontal plane.

An alternative solution approach for optimal control problems is to discretize the problem in time using a suitable discretization scheme and apply nonlinear optimization. In P[RAI96a], we describe two discretization schemes, direct collocation with cubic splines, and a method based on differential inclusions, and apply them to realistic aircraft trajectory optimization problems. The latter approach eliminates the control variables from the optimization procedure, which might be beneficial in problems involving singular control arcs. Collocation approach is also applied in P[HOF00] to find glide range optimal maneuvering strategies after an aircraft engine failure.

The robustness of the discretization methods makes the automation of the solution process easy. P[VIR99a] presents an aircraft trajectory optimization software that utilizes the discretization methods. The software runs under Microsoft Windows and it can be used, e.g., in tactical training and experimenting. The graphical interface and the fully automated solution procedure provide a user-friendly environment for nonexperts as well.

In addition to problems modeling the flight of a single aircraft, we apply trajectory optimization in the analysis of aircraft-missile encounters in P[RAI02b], P[KAR04]. In such an engagement, the missile is assumed to employ a feedback guidance law, Proportional Navigation. Hence, the evasion problem can be formulated as an optimal control problem for the aircraft. The objective function can be, e.g., the distance by which the missile misses the aircraft or maximal distance from which the missile can be launched such that the aircraft cannot out run it.

Computational methods for pursuit-evasion games

Certain parts of air combat can be mathematically described as pursuit-evasion games. Obtaining the saddle point solution of a pursuit-evasion game has been solely based on an approach similar to the Pontryagin maximum principle. We have studied ways to extend discretization and nonlinear programming into pursuit-evasion games. In the first approach, the pursuit-evasion game is decoupled into two subproblems that are updated and solved by turns until the saddle point solution is found. The subproblems are optimal control problems that can be solved using discretization and nonlinear programming. The method is described in P[RAI00a]. In P[RAI00c], the method is applied to a game describing a visual aircraft identification process of a scout aircraft, and in R[RAI00a], P[RAI01b], the method is used in computing the capture set of an optimally guided missile.

The dynamics of the game can also be discretized at the outset to obtain a discrete saddle point problem. This problem can be understood as a bilevel programming problem where the maximization and minimization are identified with the upper and the lower level problems, respectively. A feasible direction method to solve the problem is developed in R[EHT00b], P[EHT01b], see also P[EHT98]. The subproblems of the method turn out to be similar with the decomposition method presented earlier. The method is verified with a challenging game problem between a missile and an aircraft maneuvering in three dimensions. A summary of the approaches is given in R[RAI00b], P[RAI02a].

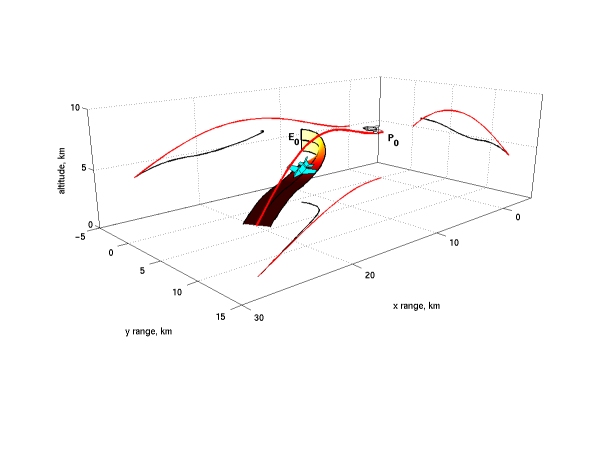Saddle point trajectories of the missile (red) and the aircraft (black) corresponding to the initial positions E0 and P0. The payoff is the final time. The projections of the trajectories are presented on the coordinate planes. The ribbon describes the aircraft's bank angle and its color specifies the dynamic pressure. Yellow corresponds to approximately 50 kPa and dark red to the allowed maximum, 80 kPa.

Modeling pilot's decision making in air combat

Simulation is a widely used method in analyzing air combat tactics and technologies. It remains as the only practical approach to model and analyze combat, if the roles of combatants are not known a priori. In air combat simulators, aircraft can be guided by a mathematical model of pilot decision making. In P[VIR99b], we construct an influence diagram model for analyzing the decision problems of a pilot during one-on-one air combat. The model describes the elements of a decision process, contains a point-mass model for the dynamics of an aircraft, and explicitly handles preferences under conditions of uncertainty. Influence diagram analysis gives information to make rational maneuvering decisions and to determine the impacts of different factors on the outcome of the maneuvering decision.

In P[VIR01a] and P[VIR04a], we extend the influence diagram approach to the modeling of the pilot's sequential maneuvering decisions. The new model provides a way to determine preference optimal flight paths in one-on-one air combat in which an adversary aircraft is flying a given trajectory. Optimal trajectories with respect to the given preference model are obtained by converting the multistage influence diagram into a discrete time dynamic optimization problem that is solved with nonlinear programming. The initial estimate for the decision variables of the problem is generated by solving a set of myopic single stage influence diagrams that anticipate the future state of the aircraft only a short planning horizon ahead.

P[VIR02], P[VIR03] and P[VIR04b] describe influence diagram game formulations modeling the maneuvering decisions of pilots in one-on-one air combat. The game models contain elements describing the rational maneuvering of the adversary as well. They produce the best maneuvering strategies with respect to the pilot's preferences and available information under the assumption that the adversary behaves in the worst possible way.

Team optimal signaling strategies

Modern fighter aircraft are equipped with a data communications system for relaying information within a group of friendly aircraft. During a many-versus-many air combat, only the most important and essential information must be transmitted in order to achieve the best possible outcome of the combat. P[VIR01b] and P[VIR05] present a prioritization model for selecting team optimal signaling strategies with respect to the overall goals of the friendly group. The model is based on a decision analytical value function which tries to capture the preferences of pilots. Uncertainty about the states of the aircraft as well as about incomplete preference statements is incorporated into the model by utilizing an interval approach. We have implemented the prioritization model in a Matlab-based software that is designed for simulating the evolution of team members' information and trajectories in an air combat game.

Simulation of aircraft maintenance and availability

Flight operations of a fleet of fighter aircraft togethter with their supporting logistics functions form a complex and dynamic environment. It connects several intrinsically complicated structures and procedures, like maintenance processes, aircraft properties and operation policies into a single system. Due to performance and availability requirements imposed on the aircraft, there is a need to better understand how the system functions as a whole in various operational environments and what is the effect of its elements to its total efficiency. In P[RAI01a] and P[MAT03], a discrete-event simulation model is constructed to study the behavior of the fligth and maintenance processes. The model describes the flight policy and the main factors of the maintenance, failure, and repair processes. Model implementation with graphical simulation software allows rapid what-if analysis for maintenance designers and offers the possibility to use the model in training of maintenance personnel.

Analysis of adjustment processes

( K. Berg, H. Ehtamo, R. P. Hämäläinen, M. Kitti )

We study adjustment processes in problems where decision makers are coordinated by one of them, or by a specific agent called a coordinator, to a desired outcome by linear equations. The coordinator adjusts the equations according to observations on decision makers' behaviour. Our research concentrates on processes for incentive design, price coordination problems and computation of Pareto-solutions in negotiations. These models have a wide variety of applications in economics and operations research.

In a multiple commodity buyer-seller game the seller gives the price tariff as an affine mapping of the buyers' actions, i.e., their buy amounts of various commodities P[EHT02]. The buyer-seller game is an example of a principal-agent game, which is a sequential game with the principal, e.g., the seller, acting first. We have studied fixed-point iteration as an adjustment rule for the principal's strategy. In byer-seller games fixed-point iteration is most often encountered price adjustment scheme in applications.

In an ongoing research our focus is on tariff design games, where the buyers' willingness to pay is not known to the seller in advance T[BER04]. Here our aim is to use minimal amount of computations to find the correct tariff. The adjustment rule describes a learning process, i.e., how the seller updates his tariff when the game is played repeatedly. Fixed-point iteration as an adjustment rule for a two-player principal-agent game has been studied in T[KIT00], P[EHT02].

Finding Walrasian equilibrium for an exchange economy is a classical coordination problem in microeconomics literature. We are developing practical methods for finding the equilibrium based on adjustment approach. Computation of Pareto-solutions in negotiations over continuous issues by using linear constraints is closely related to price adjustment. See the description below on constraint proposal methods. We focus on convergence analysis of these methods.

Multiple criteria methods for negotiations

( H. Ehtamo, R. P. Hämäläinen, V. Koskinen )

We have studied new methods for generating efficient agreements in multi-party negotiations. In these methods the problem of generating efficient agreements is decomposed into

1. ordinary multiple criteria decision making problem to be solved by each decision maker individually
2. a coordination problem for an assisting mediator.

In constraint proposal method, the mediator iteratively announces artificial plane constraints to the decision makers until their most preferred agreements coincide. This decompostition leads to an interactive procedure where the decision makers' value functions do not have to be explicitly elicited, P[EHT96a], P[EHT99a], P[EHT99b], P[VER96b], T[HEI95], P[HEI00] P[EHT01c], P[HEI01].

The problems faced by the mediator and the decision makers and the information exchange between them.

The decision makers select their most preferred agreement on the artificial plane constraint.

Another method, the method of improving directions, iteratively searches for joint improvements to tentative agreements proposed by a mediator, and step by step reach a Pareto optimal agreement.

To understand the method imagine that there are two issues A and B, two decision makers and a tentative agreement. The mediator asks the decision makers to individually criticize the tentative agreement. Based on this criticism the mediator elicits the decision maker's gradient directions and finds the jointly improving direction in the issue space, P[EHT99b], P[EHT00], P[EHT01a], P[EHT01c], T[KTT96].

Elicitation of the decision maker's gradient

The value function gradients of the decision makers and the bisecting compromise as a jointly improving direction

Models of negotiation analysis are especially suitable for e-learning because of their interactive nature. We have planned a web-site, which contains material and tools for learning mathematical models of negotiation analysis. The material consists of theory sections, case studies and assignments. It also includes quizzes for self-evaluation and video clips illustrating the use of the Joint Gains software. We describe the material and discuss students' experiences of its use in P[EHT04].

Negotiation support systems

( H. Ehtamo, R. P. Hämäläinen, V. Koskinen, J. Mustajoki )

The aim of the research is to develop practical negotiation support tools to help group decision making. The interactive methods can be used in software acting as a mediator or assisting the mediator in the generation of efficient alternatives. Applicability of the methods in real life negotiations has been investigated by applying them in environmental problems P[HÄM01a].

Joint Gains is our Web-based implementation of the method of improving directions. It allows negotiations on multiple issues between multiple parties collaborating via the Web. In practise, the system acts as a mediator asking the participants' local preferences and calculating the jointly improving directions based on this information. The participants' preference information are elicited with simple pairwise questions. Gradually, the system guides the participants towards a Pareto-optimal agreement.

Joint Gains is a part of Decisionarium, our Web site for negotiation and multicriteria decision support.

Joint Gains supports group decision making with the aid of the internet

Previous research:

Currently we do not have active research going on in these areas.

Incentives, cooperation and coordination

( H. Ehtamo, R. P. Hämäläinen )

The Stackelberg solution concept is suitable for sequential or multilevel decision problems where the different levels, decision makers, are asymmetric with respect to information. The basic idea behind this solution concept is the following. One of the decision makers, the leader, designs a strategy as a function of the available information in order to induce the other decision makers, the followers, to act in a desired manner. The problem of designing a linear strategy has been studied extensively in the literature R[EHT88a, EHT88b], P[EHT89a]. This problem is also known as the incentive design problem T[EHT89]).

(Full picture 4KB)

The joint tangent defines a linear incentive equilibrium

Linear incentive strategies can also be used to make a Pareto optimal solution an equilibrium in a dynamic context. A static counterpart is shown in the figure. Such strategies are called cooperative equilibrium strategies, or incentive equilibrium strategies. Recent results on cooperative equilibria have been presented in (R[EHT88a, b], P[EHT89a, EHT89e]). Cooperative equilibria have a fruitful application area in various multiagent resource management and environmental problems (P[EHT93a, EHT95a], P[KAI88b, KAI90c], KAI95a], KAI95d], P[HÄM89a, HÄM90c]).

Intertemporal bargaining

( H. Ehtamo, J. Ruusunen )

In the literature on axiomatic bargaining, the contracting problem between two or more decision makers has been analyzed mainly for static games, and the intertemporal nature of contracting has been totally ignored. However, many real life contracts cover multiple time periods and the intertemporal effects become an essential part of the contract design problem.

We have considered intertemporal bargaining in the presence of exogenous uncertainty P[EHT89d], EHT91], P[RUU91a]), and shown that the cooperative policy can be defined by applying dynamic programming P[EHT95c], R[EHT90]. However, this is possible only if the bargaining solution is time consistent. If this is the case, the cooperative policy can be determined in a feedback from as a function of the decision makers' expected cumulative gains.

We have also shown a very interesting relation between time consistency and the axioms of the bargaining model P[EHT96d], P[EHT95b], R[EHT93]. Namely, it turns out that time consistency is equivalent with the independence of irrelevant alternatives property of the bargaining solution. This is the property which has been most difficult to motivate in the bargaining theory literature.

In practice, the basic weakness of applying dynamic programming is the fact that it is computationally complex. Therefore we have developed an adaptive method for solving computationally complex multi-period bargaining problems which are characterized by non time separable conditions for the cooperative outcome P[EHT88b, EHT89b, EHT89c], R[EHT90]). For an application of this theory see Electricity exchage.

Distributed methods to compute Pareto optimal solutions

( H. Ehtamo, P. Heiskanen, R.P. Hämäläinen, M. Verkama )

The solution concept used in multiple criteria optimization is Pareto optimality: a deviation from a Pareto optimal solution necessarily implies lower profits (higher costs) for at least one of the decision makers. We have studied distributed computation of Pareto optimal solutions and developed interactive algorithms for solving Pareto points of games (P[EHT93b, EHT96a, EHT96b], T[VER94], P[VER96b]). Distributed algorithms can be used even if the players do not know each others' objective functions. This kind of methods are highly interesting because they could be used in real world game situations like negotiations, that are typically characterized by incomplete information P[HEI99], P[HEI01].

We have also applied distributed computation and coordination schemes to Stackelberg games, where the leader uses a pricing strategy which leads the followers to allocate a resource optimally P[HÄM95d], P[HÄM96c], P[HHE].

Coordination and games in multi-agent systems

( H. Ehtamo, R.P. Hämäläinen, J. Parantainen, M. Verkama )

The work on distributed computation of Pareto optimal and Stackelberg solutions is closely related to certain problems of distributed artificial intelligence (DAI). In particular, our methods could provide a solution when distributed autonomous agents have to cooperate to solve a joint problem P[VER92]. The methods could be used to calculate efficient actions, and the resulting incentive strategies could be used to coordinate the agents. We have also analyzed the collective behavior of reactive agents in an agent society P[VER94] Asynchronous reaction processes are of special interest because they can be more stable than their synchronous counterparts. These have lead us to study stochastic models of asynchronous computation P[VER96c].

Hierarchical agent models include Stackelberg games where the leader's objective is to maximize social welfare of a multi-agent system under incomplete information of the follower agents' goals. We have especially considered resource allocation and distribution problems and applied price coordination mechanism to solve the leader's problem P[HÄM97b]. The price coordination idea has been applied to problems in electricity markets T[PAR94], and we have developed an agent-based modeling software Power Agents P[HÄM95d] for the analysis of the electricity distribution problem.

Statistical simulation

( P. Laininen )

The increase in computation power has established the Monte Carlo methods in statistical analysis. Efron's bootstrap idea from 1979 is to make statistical experiments with the computer by generating random numbers from estimate of a distribution instead of using its analytical model. This approach makes possible to omit many assumptions about the models and to evaluate distributions of statistics which are too complicated to treat theoretically.

In our investigation the simulation technique has been introduced into multiple comparison of two or more distributions. The hypothesis that all the studied samples come from the same distribution is tested using the Mallows 1-distance as the test statistic. This statistic is by its nature very universal compared to the statistics conventionally used in this problem.

The multiple comparison problem is studied and a stagewise algorithm for multiple comparison by the Mallows 1-distance bootstrap is given. The conventional methods of grouping samples and their underlying distributions work with the pairwise comparison of samples. We introduce a bootstrap procedure for dividing the samples and distributions into maximal groups. The main hypothesis to be tested is that there is one group only, and this hypothesis is tested against the alternative that there are more than one separate group R[LAI96a].

Large scale multiobjective optimization

( K. Tarvainen )

In the practical design and optimal control of systems there has been increasing interest to replace single criterion optimization by multiple objective analysis. A special class under study in these multicriteria problems are large scale systems which can be decomposed into subsystems in the mathematical analysis. Dr. Tarvainen has studied such systems extensively, and he is one of the authors of the monograph P[HAI90], which gives a comprehensive account of the main results in this field.

Robust control in resource economics

( V. Kaitala )

A project dealing with robust control considers a class of resource management problems in which the management objective is to minimize fluctuations in resource economics P[KAI89c, KAI90b, KAI91a, KAI91b, KAI92b, HIL94]. Stabilizing management policies consist of memoryless state feedback control strategies for a class of discrete-time resource models which contain unknown but bounded fluctuations. The theory is based on conditions developed for a Lyapunov type stability of sets. The design of the stabilizing policies is illustrated by simulation examples from resource economics. A project dealing with periodic optimal solutions studies a class of continuous-time optimization models in which only one of two state variables can be controlled directly. The purpose of the study is to characterize the properties under which one can expect that periodic optimal solutions arise. Applications deal with regulation of employment, investmets, and resource level in resource economics.

Aircraft control in windshear

( V. Kaitala )

Aircraft take-off control under conditions of windshear has received attention in the control theory literature. Severe windshear may cause difficulties during aircraft take-off; it has been a major cause of at least 30 aircraft accidents during the last two decades. We have studied the controlled take-off of an aircraft flying through an unavoidable windshear P[KAI91c], P[KAI91d]. The design of the take-off control schemes (memoryless state feedback control strategies) is carried out by applying a theory of deterministic control of uncertain systems.