Kimmo Berg
Roima Intelligence
Stochastic Games
A stochastic game (Shapley 1953) consists of multiple states: one game played at each stage and stochastic transitions between the states that may depend on the players' actions. Stochastic games extend both Markov Decision Processes (where there is only one player) and repeated games (the same game played over and over again). One of the open questions is under what conditions a stochastic game has an equilibrium. Discounted stochastic games have an equilibrium in stationary strategies (Fink 1964, Takahashi 1964). Below is an example of two-player stochastic game with different prisoner's dilemmas in each state (Kitti 2012). The number sign # denotes the action profiles after which the state stays deterministically the same. Otherwise, the future state is randombly drawn.
| L | R | L | R | |||||
| state 1 | T | 4,4 # | 0,5 # | state 2 | T | 0,0 | -4,1 | |
| B | 5,0 # | 1,1 | B | 1,-4 | -3,-3 # |
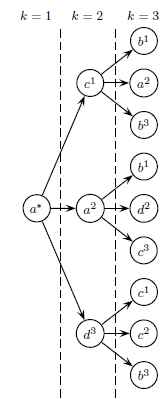
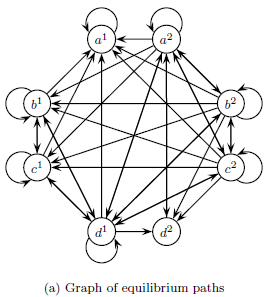
In Berg "Characterization of equilibrium paths in discounted stochastic games" the elementary subpaths (the basic elements of which the equilibrium paths consists of) and the methods for computing pure-strategy subgame-perfect equilibria are extended to stochastic games. The elementary subpaths are trees since the actions can be planned differently for each possible future state where the game may evolve. This adds much more complexity to the set of equilibria and the computation. Also, the set of solutions is much bigger in stochastic games compared to repeated games. The left pic below shows an example of an elementary subpath in a game with three states, where action profile a is played in the first period. In the second period, c is played if the game evolves to state 1, a in state 2 and d in state 3. In the third period, there are nine history-dependent action profiles. The right pic shows an example graph of all possible equilibrium paths. The transitions are stochastic and depend on which state the game evolves.
 |
 |
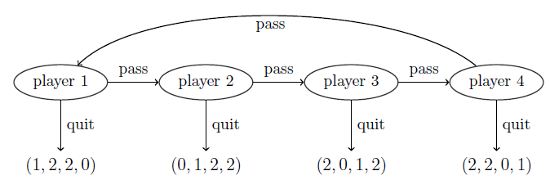
Berg et al. (2015) examine the following quitting game where five coins are divided among four players. In each round, it is one player's turn with two options: to quit or to pass. If he quits he earns 1 coin, the next two players get 2 coins each and the remaining player gets nothing. The players act in turns starting from player 1. The players may randomize between the two choices and the game has two subgame-perfect Nash equilibria in stationary strategies. In one solution, all players quit deterministically with probability 1 and the players get payoffs (1,2,2,0). The second solution is more interesting where each player quits on every round they are called to act with probability (3-√5)/2=2-φ≈0.38, where φ=(1+√5)/2 is the golden ratio. The players' expected payoffs are (1,3-φ,φ,1). Thus, the fifth extra coin is divided between players 2 and 3 given by the proportion of golden ratio! The paper also find golden and silver ratios in other similar games with different payoffs and more than four players.