Kimmo Berg
Roima Intelligence
Minimum Equilibrium Payoffs in Repeated Games
The computation of repeated game equilibria requires that the minimum equilibrium payoffs are known. These payoffs provide the credible threats, i.e., the values that the players receive if they deviate from the equilibrium strategies. In many games, the minimum payoffs are easy to find but they can be complicated in some games. Berg "Extremal pure strategies and monotonicity in repeated games" proposes a simple modification of Berg and Kitti (2013) algorithm to find the minimum payoffs and constructs a game where a path is no longer equilibrium when the players become more patient. This is a big result as intuition tells that the set of equilibria should be monotone in the players' discount factors. This finding relies on the fact that the punishment payoffs may increase when the players become more patient. This means that the threats may get weaker and this may change the players' incentives. The intuitive result is, however, obtained since it is proven that the set of equilibria is monotone if the punishment payoffs do not increase, which gives a sufficient condition for the monotonicity.
One of the most interesting applications of repeated games are oligopoly models. The following duopoly game was introduced in Abreu (1988). Two firms decide their output levels: low (L), medium (M) and high (H). The nine action profiles are denoted by the alphabets a-i and the Nash equilibrium is e giving payoffs 7,7.
| L | M | H | |
| L | 10,10 (a) | 3,15 (b) | 0,7 (c) |
| M | 15,3 (d) | 7,7 (e) | -4,5 (f) |
| H | 7,0 (g) | 5,-4 (h) | -15,-15(i) |
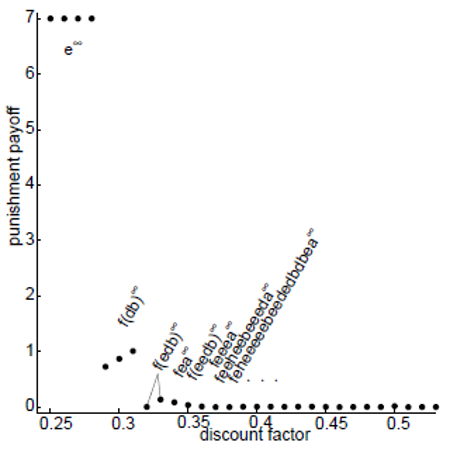
In Berg "Extremal pure strategies and monotonicity in repeated games", the minimum payoffs are computed for different discount factors (see the figure below). We can observe that the punishment payoffs are not monotone when the common discount factor is between 0.29 and 0.31. We can also see that the Nash equilibrium is the only solution when the players are impatient and the minimum payoff falls close to the minimax payoff of 0 when the players become more patient. When d>0.53, it is possible to play c infinitely and the minimum payoff is exactly 0 for these discount factor values. We can also observe that the punishment paths may be really long.
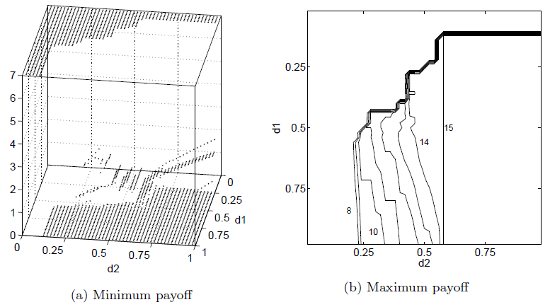
Berg and Kärki "An algorithm for finding the minimum pure-strategy payoffs in repeated games" presents an improved algorithm that is based on the idea of branch-and-bound. The new algorithm can find the minimum payoffs for general games with all values of discount factors. The earlier algorithm could only solve games where the set of equilibria was small, i.e., when the discount factors were small enough. The following figures show the minimum payoff of player 1 as a function of both players discount factors d1 and d2. With the new method, it is also possible to compute the Pareto efficient solution and the right figure shows the maximum payoff of player 1 in the duopoly game. We can see that the maximum payoffs depend on both players minimum payoffs. When the minimum payoffs are low, it is possible to get solutions with high payoffs.