Kimmo Berg

Roima Intelligence

Nonlinear Pricing

Nonlinear pricing describes a problem between a seller and multiple buyers. The selling firm produces a product with possibly multiple qualities. The firm has a cost function that tells how much it costs to produce a unit of product with certain quality. Each buyer type is represented with a utility function and there can be multiple buyers with the same type. The firm designs a menu of quality-price bundles (see pic below): each bundle consists of a distinctive product with certain qualities and its price. The buyers may choose any bundle they wish to consume or not buy anything at all, and typically a buyer only wishes to buy one bundle of the product. The problem can be seen as an optimization problem where the firm has to set the qualities for each type and set the prices as high in order to maximize its profits. The firm needs to take into account that the buyers may choose any bundle they wish. If the price of the bundle is increased too much, the buyers rather take some other bundle.

Nonlinear pricing problem is an example of more general game setting where the players have incomplete information about the other players. These problems are also called optimal screening, mechanism design, adverse selection and principal-agent problems. The problem was formulated in 1970s by Spence and the problem has been studied by Wilson (1993), Armstrong (1996) and Rochet and Chone (1998). For example, an insurance company provides insurance for a driver whose driving skills are only privately known.

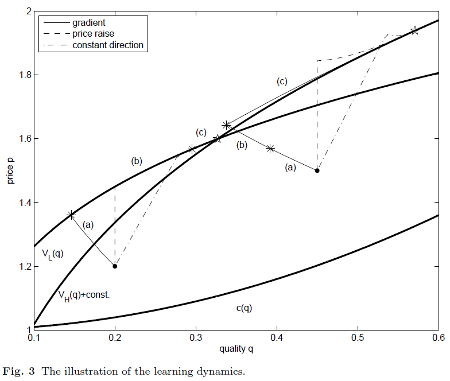
In Berg and Ehtamo (2009) and Ehtamo et al. (2010) we examine how to find the optimal solution to the nonlinear pricing problem when the seller does not know the buyers' utility functions. The firm can set different tariffs or menus and observe what the buyers choose. The task is to learn the optimal bundles by adjusting the qualities and the prices. In Berg and Ehtamo (2010) we examine continuous learning dynamics and observe that the gradient method, where the firm adjusts the bundles in the direction where the profit increases the most, is not the best way overall to learn the bundles.

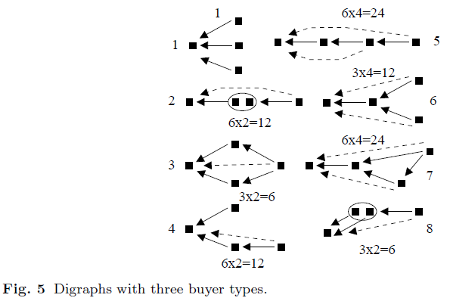
In Berg and Ehtamo (2008,2010) we describe the nonlinear pricing problem as an optimization problem and interpret its active constraints or Lagrange multipliers. The multipliers convey information about the optimal solution: what types "envy" what other bundles and how the bundles are related. Similar envy graphs have been discovered by Nahata et al. (2001,2004). In Berg (2013) it is examined how many different graphs there are when the number of buyer types is given and how different assumptions affect the number of graphs.